
Zahra Faraei
Assistant Professor at Physics Department
Institute for Advanced Studies in Basic Sciences (IASBS), Zanjan, Iran
Contact information
z.faraei iasbs.ac.ir
zahra.faraei gmail.com
+98 24 3315 2249
Institute for Advanced Studies in Basic Sciences (IASBS), No. 444, Prof. Yousef Sobouti Blvd., Zanjan 45137-66731, Iran
Research Interests
I am a theoretical physicist working on various aspects of quantum condensed matter physics, with a focus on superconductivity and topology. I study how the phase transition and the mass gap generation in superconductors are influenced by the presence of topological features, such as edge states, Majorana fermions, and fractional statistics. I explore the different pairing symmetries and the resulting gap structures in Weyl superconductors, which are materials that host massless Weyl fermions. I also investigate how external fields can manipulate and detect these superconductivities. I investigate the possibility of creating and manipulating half-vortices, which are vortices that carry half of the quantum of flux, in a network of Weyl superconductors. I am also interested in the exotic properties and applications of these half-vortices, such as fractional statistics, non-Abelian braiding, and the chiral Josephson effect.
Current Projects
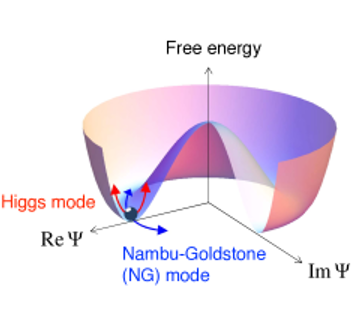
Anderson-Higgs mechanism in topological superconductors
The Higgs-Anderson mechanism is a general phenomenon that occurs when a system with a local symmetry undergoes a phase transition and acquires a mass gap. In superconductors, this mechanism explains the Meissner effect, which is the expulsion of magnetic fields from the interior of the material. The Higgs-Anderson mechanism also implies the existence of a collective excitation called the Higgs mode, which is related to the fluctuations of the order parameter.
Topological superconductors are a special class of superconductors that have non-trivial topological properties, such as edge states, Majorana fermions, and fractional statistics. These properties are protected by symmetries and are robust against local perturbations. Topological superconductors can be realized in various systems, such as spin-orbit coupled materials, heterostructures, and cold atoms.
The Higgs-Anderson mechanism in topological superconductors has some unique features that distinguish it from conventional superconductors. For example, the Higgs mode can couple to other excitations, such as magnons or surface plasmons, and exhibit novel phenomena, such as hybridization, amplification, or resonance. The Higgs mode can also be influenced by the presence of topological defects, such as vortices or domain walls, and reveal information about the underlying symmetry and topology of the system.
This is a very active and fascinating research area with potential applications in quantum information, metrology, and nanotechnology.
Different types of superconductivities in Weyl superconductors
Superconductivity is a phenomenon in which a material can conduct electricity without any resistance below a certain critical temperature. Superconductors can be classified into different types based on their properties and mechanisms.
Weyl superconductors are a new class of superconductors that emerge from Weyl semimetals, which are materials that have linear dispersion around isolated points in the momentum space called Weyl nodes. Weyl nodes have a definite chirality, which means they act like sources or sinks of Berry curvature, a geometric quantity that measures the twisting of the electronic wave functions. Weyl semimetals also have exotic surface states called Fermi arcs, which connect the projections of the Weyl nodes on the surface.
When Weyl semimetals become superconducting, they exhibit novel features that are not found in conventional superconductors. For example, the superconducting gap function, which describes the energy cost of breaking a Cooper pair, can have point nodes that are protected by symmetry or topology. These point nodes can be manipulated by tuning the tilt of the Weyl nodes, which affects their separation and location in the momentum space. The point nodes also give rise to low-energy excitations called Bogoliubov-Weyl fermions, which are analogs of the Weyl fermions in the normal state. Moreover, the surface of Weyl superconductors can host chiral Majorana modes, which are exotic quasiparticles that are their antiparticles and obey non-Abelian statistics. These modes can be detected by various probes, such as tunneling spectroscopy, Josephson effect, or thermal transport34.
In this project, we aim to explore the different types of superconductivities in Weyl superconductors and their physical consequences. We will use theoretical methods, such as mean-field theory, Green’s function technique, and topological invariant calculation, to study the phase diagram, the electronic structure, the vortex physics, and the surface states of Weyl superconductors. We will also compare our results with existing and future experiments and propose new ways to realize and manipulate Weyl superconductivity in various systems.
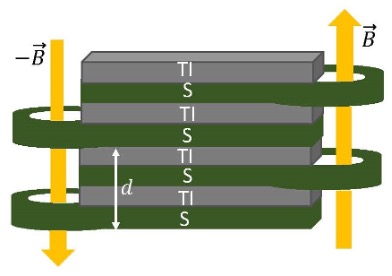
Half-vortices in Weyl superconductor Josephson arrays
A Josephson array is a network of superconducting islands connected by weak links, such as tunnel junctions or nanowires. A Josephson array can exhibit various collective phenomena, such as phase transitions, quantum fluctuations, and vortex dynamics. A vortex is a topological defect in the superconducting order parameter that carries a quantized magnetic flux.
Weyl superconductors are a new class of superconductors that emerge from Weyl semimetals, which are materials that have linear dispersion around isolated points in the momentum space called Weyl nodes. Weyl superconductors can have different types of pairing symmetries, such as scalar, pseudoscalar, vector, or axial vector. These pairing symmetries can be tuned by external parameters, such as magnetic field, strain, or doping.
In this project, we investigate the possibility of creating and manipulating half-vortices in a Josephson array made of Weyl superconductors. A half-vortex is a vortex that carries half of the quantum of flux and has a fractional winding number. Half-vortices can arise when the superconducting order parameter has both scalar and pseudoscalar components, which can be controlled by the flux biasing of the weak links. Half-vortices have exotic properties, such as fractional statistics, non-Abelian braiding, and the chiral Josephson effect.
We use theoretical methods, such as mean-field theory, renormalization group, and numerical simulation, to study the phase diagram, the stability, the transport, and the braiding of half-vortices in Weyl superconductor Josephson arrays. We also propose realistic experimental setups to realize and detect half-vortices in these systems.
Entanglement and topology
Entanglement and topology are two fundamental concepts in quantum physics that reveal the richness and complexity of quantum states.
Entanglement is a phenomenon in which quantum particles share information and correlations across space and time, even when they are separated by large distances. Topology is a branch of mathematics that studies the global and invariant properties of shapes and spaces, such as holes, twists, and knots.
Entanglement and topology have profound implications for various fields of physics, such as condensed matter, quantum information, quantum gravity, and high-energy physics. They can lead to novel phases of matter, such as topological insulators, quantum Hall states, and quantum spin liquids, that have exotic properties and applications. They can also provide new insights into the nature of space-time, black holes, and quantum gravity.
In this project, we explore the connections and interplay between entanglement and topology in different quantum systems. We use theoretical tools, such as entanglement measures, topological invariants, and quantum field theory, to investigate how entanglement and topology can be characterized, quantified, manipulated, and detected. We also compare our results with experimental observations and propose new ways to realize and control entangled and topological states in various platforms.

Weyl antiferromagnets
Weyl antiferromagnets are magnetic materials that host Weyl fermions, which are massless particles that behave like monopoles of Berry curvature in momentum space. Weyl fermions, such as chiral antiferromagnets, can be realized as low-energy excitations in systems that break both time-reversal and inversion symmetries. Weyl fermions can form isolated points or closed loops in the Brillouin zone, which are called Weyl nodes or Weyl nodal loops, respectively. These topological features give rise to various anomalous transport phenomena, such as the chiral magnetic effect, the chiral anomaly, and the planar Hall effect.
In this project, we aim to study Weyl antiferromagnets using theoretical methods. We use group theory to identify candidate materials that can host different types of Weyl nodes and nodal loops, such as Mn3Sn. We write a Hamiltonian for Weyl antiferromagnets that describes the interaction between the magnetic background and the relativistic Weyl fermions. We use this Hamiltonian to study the transport features and the linear response of these systems under external fields or strain. We also explore the emergence of novel quasiparticles, such as Weyl magnons, in these systems.
